dislocations

towards QM accuracy

Dislocations are extended line defects which carry plastic deformation in crystalline materials . Understanding and optimizing dislocation behaviour by characterising dislocation interaction with point defects is a central topic in computational metallurgy . For this task, ab initio calculations, specifically density functional theory (DFT) , are essential to capture dislocation core structures and complex bonding to impurity elements. However, the computational cost of DFT typically scales with the number of atoms as O(N3) for metallic systems, which limits its direct applicability to the study of extended defects. Within this project I develop and apply hybrid QM/MM methods which allow to study unfeasibly large systems with ab initio accuracy.

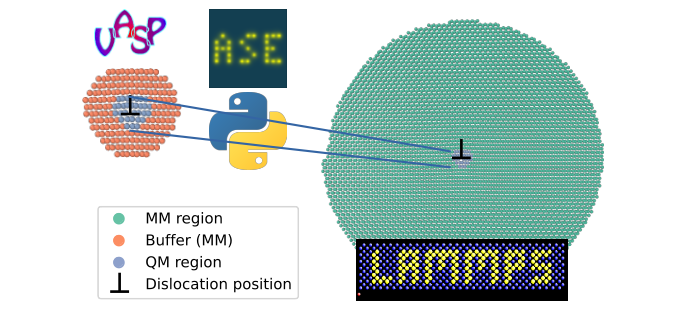
QM/MM coupling scheme.

Hybrid QM/MM coupling scheme practically requires running two simulations in parallel: LAMMPS for MM part and VASP for DFT cell while the coupling is implemented with python ASE interface. The QM/MM forcs FQM/MM is obtained by mixing MM force FLAMMPS with ab initio force FVASP with simple relation:

FQM/MM={FVASP,X∈QMFLAMMPS,otherwise

where X is atomic coordinates vector and QM denotes QM region shown with blue color. The position of the atoms are then updated according to the QM/MM force FQM/MM during ionic minimisation. An important aspect of hybrid QM/MM simulations is the need to have a buffer of sacrificial DFT atoms (shown with orange color), suitably large to protect the target cluster from electronic free surface effects.

This method provides a unique tool to study dislocations with ab initio accuracy . Moreover, further extension of the capabilities is possible by combination of the method with recent developments in machine learning based force fields . Exploration of this possibility is the main topic of this project.

Footnotes

    References

    1. Theory Of Dislocations
      Hirth, J.P. and Lothe, J., 1991. Malabar, FL Krieger.
    2. Quantitative prediction of solute strengthening in aluminium alloys  [link]
      Leyson, G.P.M., Curtin, W.A., Hector, L.G. and Woodward, C.F., 2010. Nature materials, Vol 9(9), pp. 750--755. Nature Publishing Group.
    3. Electronic Structure: Basic Theory and Practical Methods
      Martin, R.M., 2004. Cambridge University Press.
    4. Hybrid atomistic simulation methods for materials systems  [link]
      Bernstein, N., Kermode, J.R. and Csanyi, G., 2009. Reports on Progress in Physics, Vol 72(2), pp. 026501. IOP Publishing.
    5. Computing energy barriers for rare events from hybrid quantum/classical simulations through the virtual work principle  [link]
      Swinburne, T.D. and Kermode, J.R., 2017. Phys. Rev. B, Vol 96(14), pp. 144102. American Physical Society.
    6. Hybrid quantum/classical study of hydrogen-decorated screw dislocations in tungsten: Ultrafast pipe diffusion, core reconstruction, and effects on glide mechanism  [PDF]
      Grigorev, P., Swinburne, T.D. and Kermode, J.R., 2020. Phys. Rev. Materials, Vol 4(2), pp. 023601. American Physical Society.
    7. Efficient and transferable machine learning potentials for the simulation of crystal defects in bcc Fe and W  [link]
      Goryaeva, A.M., Dérès, J., Lapointe, C., Grigorev, P., Swinburne, T.D., Kermode, J.R., Ventelon, L., Baima, J. and Marinica, M., 2021. Phys. Rev. Materials, Vol 5(10), pp. 103803. American Physical Society.