Extremely proud to be a part of an amazing achievement of my brother Volodia! 
An article titled “Optically Triggered Néel Vector Manipulation of a Metallic Antiferromagnet Mn\(_2\)Au under Strain” has been accepted for publication in ACS Nano journal and is now avialable online. The preprint version of the manuscript can be obtained via arXiv as well as HAL open archive. My brother Vladimir Grigorev is the first author of this publication! The article demonstrates the local manipulation of direction of the staggered magnetization of an antiferromagnetic thin film using combination of strain and laser pulses. The motivation of the study is testing the capabilities of the material for future ultra fast high-density memory spintronic devices.
The experimental results are backed up by a profound theoretical analysis as well as computational modelling. The article represents an extraordinary example of successful collaboration between few teams with various backgrounds. My humble role was to perform Density Functional Theory calculations of magneto-elastic coupling constant \(B_{me}\) that shows how preferable orientation of magnetic moments of the atoms changes with applied strain.
Mn\(_2\)Au is a metallic collinear antiferromagnet with body central tetragonal crystall structure. Easy directions are along \(\langle 110 \rangle\) axis, this means that in the ground state magnetic moments of Mn atoms lie in \((001)\) plane and are oriented along one of the \(\langle 110 \rangle\) directions as shown in the figure below. If a tensile strain along one of these easy directions (say \(\varepsilon _{110}\)) is applied does it favour the spin orientation along the strain (\([110]\) direction) or perpendicular to it (\([\bar110]\) direction)? It is possible to answer this question by calculating the energy difference between strained configurations with two spin orientation \(\Delta E = E([\bar110]) - E([110])\) as schematically shown below.
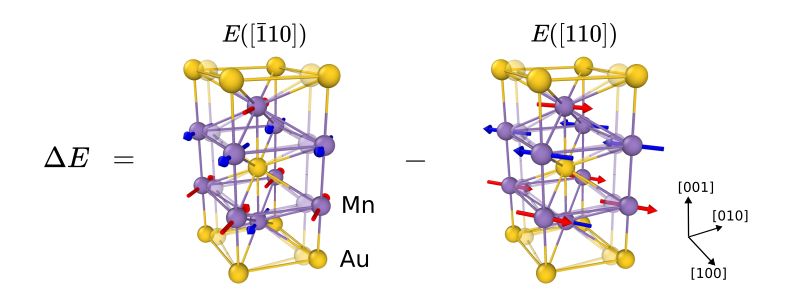
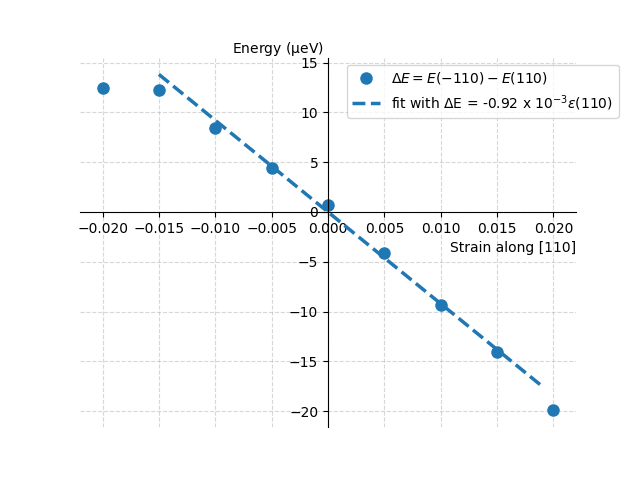
It is important to note the energies of ground states \(E([\bar110])\) and \(E([110])\) have negative values indicating binding of the structure. Lower energy means more stable configuration. Thus, if the \(\Delta E\) is positive, it means that the structure with magnetic moments parallel to the strain has lower energy and thus is more favourable. If the value is negative, then the orientation of magnetic moments perpendicular to the strain is preferred. As can be seen from the plot below, \(\Delta E\) is negative for the positive values of strain along \([110]\) direction \(\varepsilon _{110}\). This means that the tensile strain favours perpendicular orientation of magnetic moments. By making a linear fit of this results we obtain the magneto elastic constant of \(B_{me}\) = -0.92 meV per formula unit (one unit cell). This value means that one percent of strain results in 9.2 \(\mu\)eV of magnetic anisotropy per formula unit between easy directions \(\langle 110 \rangle\).
More details about the calculations including VASP parameters, convergence test and other quantities that were calculated can be found here. In short, I followed the methodology described in